Statsmodels
wangzf / 2022-05-02
statistical models, hypothesis tests, and data exploration
安装
依赖
- Python >= 3.7
- NumPy >= 1.17
- SciPy >= 1.3
- Pandas >= 1.0
- Patsy >= 0.5.2
- Cython
conda
$ conda install -c conda-forge statsmodels
PyPI
$ pip install statsmodels
使用
简单线性回归
statsmodels 支持模型使用以下两种风格:
- R 语言公式风格
- pandas.DataFrame/numpy array
公式风格
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
# data
data = sm.datasets.get_rdataset("Guerry", "HistData").data
print(data)
# regression model
results = smf.ols(
"Lottery ~ Literacy + np.log(Pop1831)",
data = data
).fit()
print(results.summary())
print(dir(results))
print(results.__doc__)
dept Region Department Crime_pers ... Prostitutes Distance Area Pop1831
0 1 E Ain 28870 ... 13 218.372 5762 346.03
1 2 N Aisne 26226 ... 327 65.945 7369 513.00
2 3 C Allier 26747 ... 34 161.927 7340 298.26
3 4 E Basses-Alpes 12935 ... 2 351.399 6925 155.90
4 5 E Hautes-Alpes 17488 ... 1 320.280 5549 129.10
.. ... ... ... ... ... ... ... ... ...
81 86 W Vienne 15010 ... 18 170.523 6990 282.73
82 87 C Haute-Vienne 16256 ... 7 198.874 5520 285.13
83 88 E Vosges 18835 ... 43 174.477 5874 397.99
84 89 C Yonne 18006 ... 272 81.797 7427 352.49
85 200 NaN Corse 2199 ... 1 539.213 8680 195.41
[86 rows x 23 columns]
OLS Regression Results
==============================================================================
Dep. Variable: Lottery R-squared: 0.348
Model: OLS Adj. R-squared: 0.333
Method: Least Squares F-statistic: 22.20
Date: Thu, 17 Nov 2022 Prob (F-statistic): 1.90e-08
Time: 00:01:21 Log-Likelihood: -379.82
No. Observations: 86 AIC: 765.6
Df Residuals: 83 BIC: 773.0
Df Model: 2
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 246.4341 35.233 6.995 0.000 176.358 316.510
Literacy -0.4889 0.128 -3.832 0.000 -0.743 -0.235
np.log(Pop1831) -31.3114 5.977 -5.239 0.000 -43.199 -19.424
==============================================================================
Omnibus: 3.713 Durbin-Watson: 2.019
Prob(Omnibus): 0.156 Jarque-Bera (JB): 3.394
Skew: -0.487 Prob(JB): 0.183
Kurtosis: 3.003 Cond. No. 702.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
['HC0_se', 'HC1_se', 'HC2_se', 'HC3_se', '_HCCM', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_abat_diagonal', '_cache', '_data_attr', '_data_in_cache', '_get_robustcov_results', '_is_nested', '_use_t', '_wexog_singular_values', 'aic', 'bic', 'bse', 'centered_tss', 'compare_f_test', 'compare_lm_test', 'compare_lr_test', 'condition_number', 'conf_int', 'conf_int_el', 'cov_HC0', 'cov_HC1', 'cov_HC2', 'cov_HC3', 'cov_kwds', 'cov_params', 'cov_type', 'df_model', 'df_resid', 'diagn', 'eigenvals', 'el_test', 'ess', 'f_pvalue', 'f_test', 'fittedvalues', 'fvalue', 'get_influence', 'get_prediction', 'get_robustcov_results', 'info_criteria', 'initialize', 'k_constant', 'llf', 'load', 'model', 'mse_model', 'mse_resid', 'mse_total', 'nobs', 'normalized_cov_params', 'outlier_test', 'params', 'predict', 'pvalues', 'remove_data', 'resid', 'resid_pearson', 'rsquared', 'rsquared_adj', 'save', 'scale', 'ssr', 'summary', 'summary2', 't_test', 't_test_pairwise', 'tvalues', 'uncentered_tss', 'use_t', 'wald_test', 'wald_test_terms', 'wresid']
Results class for for an OLS model.
Parameters
----------
model : RegressionModel
The regression model instance.
params : ndarray
The estimated parameters.
normalized_cov_params : ndarray
The normalized covariance parameters.
scale : float
The estimated scale of the residuals.
cov_type : str
The covariance estimator used in the results.
cov_kwds : dict
Additional keywords used in the covariance specification.
use_t : bool
Flag indicating to use the Student's t in inference.
**kwargs
Additional keyword arguments used to initialize the results.
See Also
--------
RegressionResults
Results store for WLS and GLW models.
Notes
-----
Most of the methods and attributes are inherited from RegressionResults.
The special methods that are only available for OLS are:
- get_influence
- outlier_test
- el_test
- conf_int_el
numpy array 风格
import numpy as np
import statsmodels.api as sm
# data
nobs = 100
X = np.random.random((nobs, 2))
X = sm.add_constant(X)
beta = [1, 0.1, 0.5]
e = np.random.random(nobs)
y = np.dot(X, beta) + e
# regression model
results = sm.OLS(y, X).fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.178
Model: OLS Adj. R-squared: 0.161
Method: Least Squares F-statistic: 10.51
Date: Wed, 02 Nov 2022 Prob (F-statistic): 7.41e-05
Time: 17:12:45 Log-Likelihood: -20.926
No. Observations: 100 AIC: 47.85
Df Residuals: 97 BIC: 55.67
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.4713 0.075 19.579 0.000 1.322 1.620
x1 0.1045 0.105 1.000 0.320 -0.103 0.312
x2 0.4831 0.107 4.503 0.000 0.270 0.696
==============================================================================
Omnibus: 39.684 Durbin-Watson: 1.848
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6.503
Skew: 0.096 Prob(JB): 0.0387
Kurtosis: 1.766 Cond. No. 5.09
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
详细使用
载入模块和函数
import pandas as pd
import statsmodels.api as sm
from patsy import dmatrices
数据
df = sm.datasets.get_rdataset("Guerry", "HistData").data
vars = ["Department", "Lottery", "Literacy", "Wealth", "Region"]
df = df[vars]
df = df.dropna()
df[-5:]
Department Lottery Literacy Wealth Region
80 Vendee 68 28 56 W
81 Vienne 40 25 68 W
82 Haute-Vienne 55 13 67 C
83 Vosges 14 62 82 E
84 Yonne 51 47 30 C
构造设计矩阵
y, X = dmatrices(
"Lottery ~ Literacy + Wealth + Region",
data = df,
return_type = "dataframe"
)
y[:3]
x[:3]
Lottery
0 41.0
1 38.0
2 66.0
Intercept Region[T.E] Region[T.N] ... Region[T.W] Literacy Wealth
0 1.0 1.0 0.0 ... 0.0 37.0 73.0
1 1.0 0.0 1.0 ... 0.0 51.0 22.0
2 1.0 0.0 0.0 ... 0.0 13.0 61.0
[3 rows x 7 columns]
模型
model = sm.OLS(y, X)
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Lottery R-squared: 0.338
Model: OLS Adj. R-squared: 0.287
Method: Least Squares F-statistic: 6.636
Date: Wed, 02 Nov 2022 Prob (F-statistic): 1.07e-05
Time: 17:12:43 Log-Likelihood: -375.30
No. Observations: 85 AIC: 764.6
Df Residuals: 78 BIC: 781.7
Df Model: 6
Covariance Type: nonrobust
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 38.6517 9.456 4.087 0.000 19.826 57.478
Region[T.E] -15.4278 9.727 -1.586 0.117 -34.793 3.938
Region[T.N] -10.0170 9.260 -1.082 0.283 -28.453 8.419
Region[T.S] -4.5483 7.279 -0.625 0.534 -19.039 9.943
Region[T.W] -10.0913 7.196 -1.402 0.165 -24.418 4.235
Literacy -0.1858 0.210 -0.886 0.378 -0.603 0.232
Wealth 0.4515 0.103 4.390 0.000 0.247 0.656
==============================================================================
Omnibus: 3.049 Durbin-Watson: 1.785
Prob(Omnibus): 0.218 Jarque-Bera (JB): 2.694
Skew: -0.340 Prob(JB): 0.260
Kurtosis: 2.454 Cond. No. 371.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
result.params
result.rsquared
Intercept 38.651655
Region[T.E] -15.427785
Region[T.N] -10.016961
Region[T.S] -4.548257
Region[T.W] -10.091276
Literacy -0.185819
Wealth 0.451475
dtype: float64
0.337950869192882
模型诊断和测试
sm.stats.linear_rainbow(result)
print(sm.stats.linear_rainbow.__doc__)
# (F-statistic, p-value)
(0.8472339976156916, 0.6997965543621643)
sm.graphics.plot_partregress(
"Lottery",
"Wealth",
["Region", "Literacy"],
data = df,
obs_labels = False
)
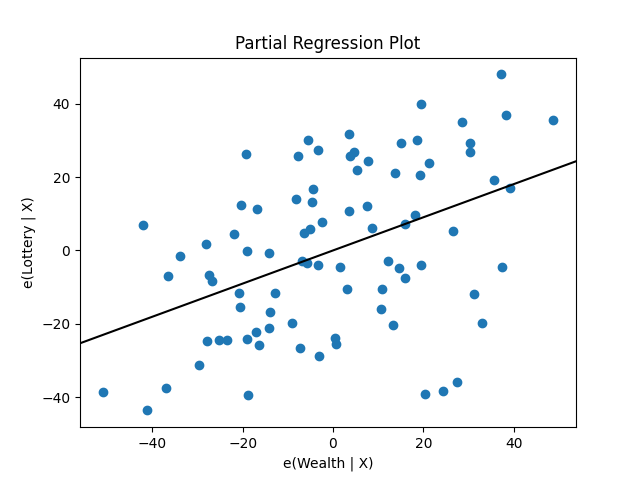
回归与线性模型
时间序列分析
ARMA
statsmodels.tsa
- Univariate
- autoregressive models(AR)
- vector autoregressive models(VAR)
- autoregressive moving average models(ARMA)
- Non-linear models
- Markov switching dynamic regression and autoregression
- 描述性统计量
- autocorrelation: 自相关图
- partal autocorrelation: 偏自相关图
- periodogram: 周期图
- ARMA 相关的理论属性或过程
- 使用 AR 和 MA 滞后多项式(lag-polynomials)的方法
- 相关的统计检验
- 一些有用的函数
statsmodels.tsa 命名空间中的模块结构:
- stattools
- ar_model
- arima.model
- statspace
- vector_ar
- arma_process
- sandbox.tsa.fftarma
- tsatools
- filters
- regime_switching
估计
- 极大似然估计、条件极大似然估计(exact or condition Maximum Likelihood)
- 条件最小二乘(conditional least-quares)
- 卡尔曼滤波(Kalman Filter)或直接滤波器(direct filters.)
指数平滑 Exponential Smoothing
Holt Winter’s Exponential Smoothing
Simple Exponential Smoothing
Holt’s Exponential Smoothing
自相关系数和偏自相关系数计算
import statsmodels.api as sm
X = [2, 3, 4, 3, 8, 7]
print(sm.tsa.stattools.acf(X, nlags = 1, adjusted = True))
[1, 0.3559322]
自相关图和偏自相关图绘制
import numpy as np
import pandas as pd
import akshare as ak
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
np.random.seed(123)
# -------------- 准备数据 --------------
# 白噪声
white_noise = np.random.standard_normal(size=1000)
# 随机游走
x = np.random.standard_normal(size=1000)
random_walk = np.cumsum(x)
# GDP
df = ak.macro_china_gdp()
df = df.set_index('季度')
df.index = pd.to_datetime(df.index)
gdp = df['国内生产总值-绝对值'][::-1].astype('float')
# GDP DIFF
gdp_diff = gdp.diff(4).dropna()
# -------------- 绘制图形 --------------
fig, ax = plt.subplots(4, 2)
fig.subplots_adjust(hspace = 0.5)
plot_acf(white_noise, ax = ax[0][0])
ax[0][0].set_title('ACF(white_noise)')
plot_pacf(white_noise, ax = ax[0][1])
ax[0][1].set_title('PACF(white_noise)')
plot_acf(random_walk, ax = ax[1][0])
ax[1][0].set_title('ACF(random_walk)')
plot_pacf(random_walk, ax = ax[1][1])
ax[1][1].set_title('PACF(random_walk)')
plot_acf(gdp, ax = ax[2][0])
ax[2][0].set_title('ACF(gdp)')
plot_pacf(gdp, ax = ax[2][1])
ax[2][1].set_title('PACF(gdp)')
plot_acf(gdp_diff, ax = ax[3][0])
ax[3][0].set_title('ACF(gdp_diff)')
plot_pacf(gdp_diff, ax = ax[3][1])
ax[3][1].set_title('PACF(gdp_diff)')
plt.show()
